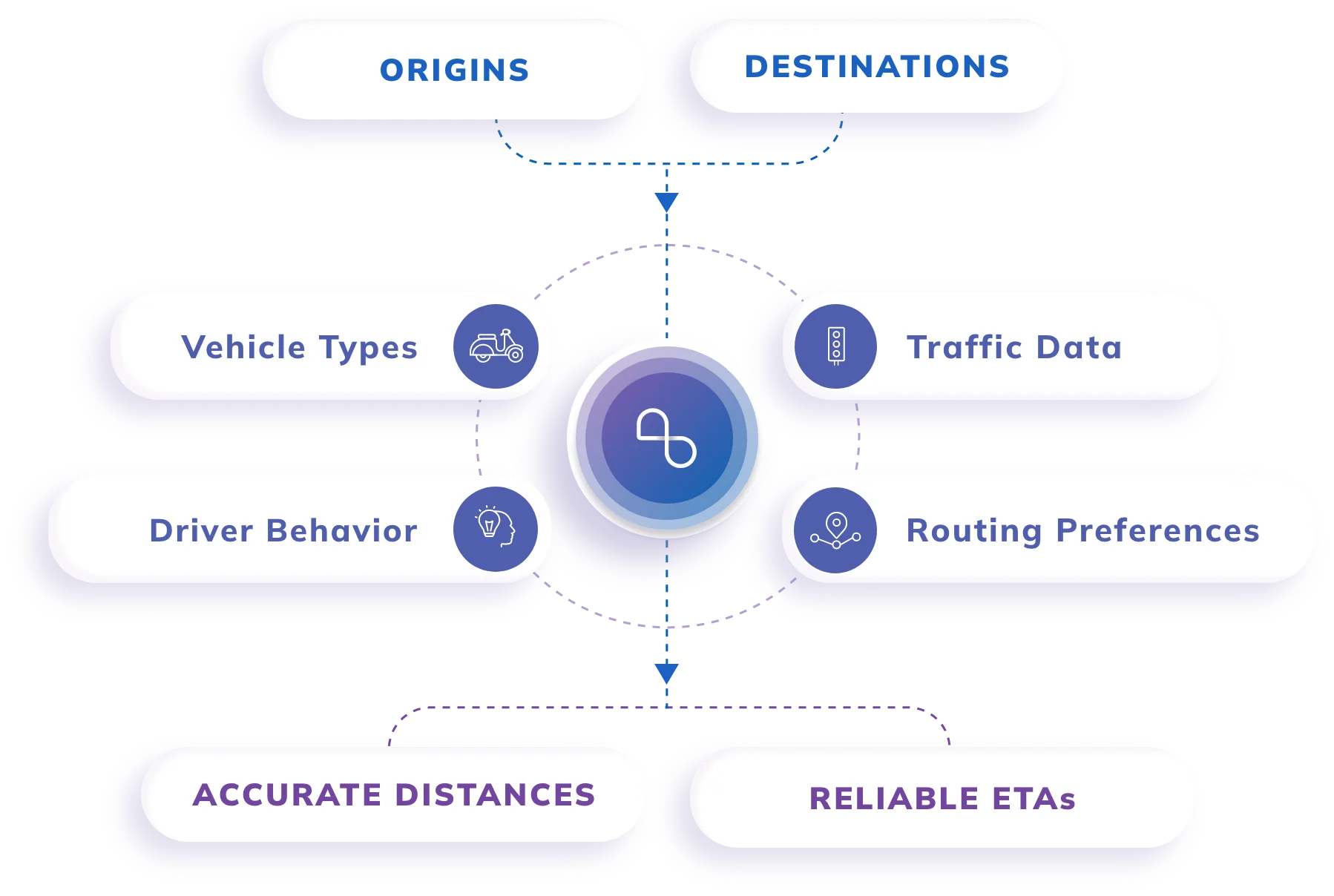
Key Features
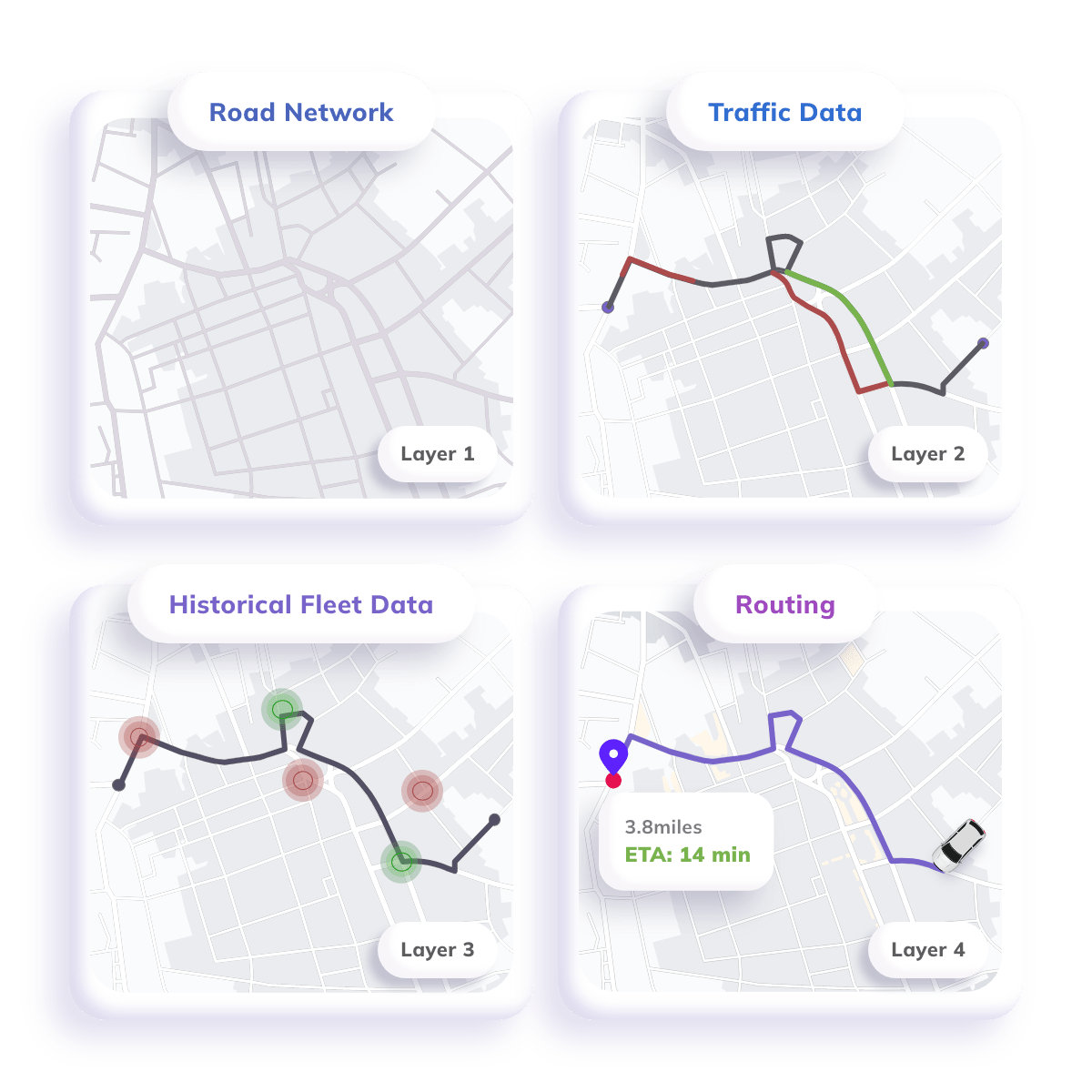
Comprehensive Map and Traffic Data
We integrate map and traffic data from a variety of data partners to ensure reliable ETAs for your business in its region(s) of operation.
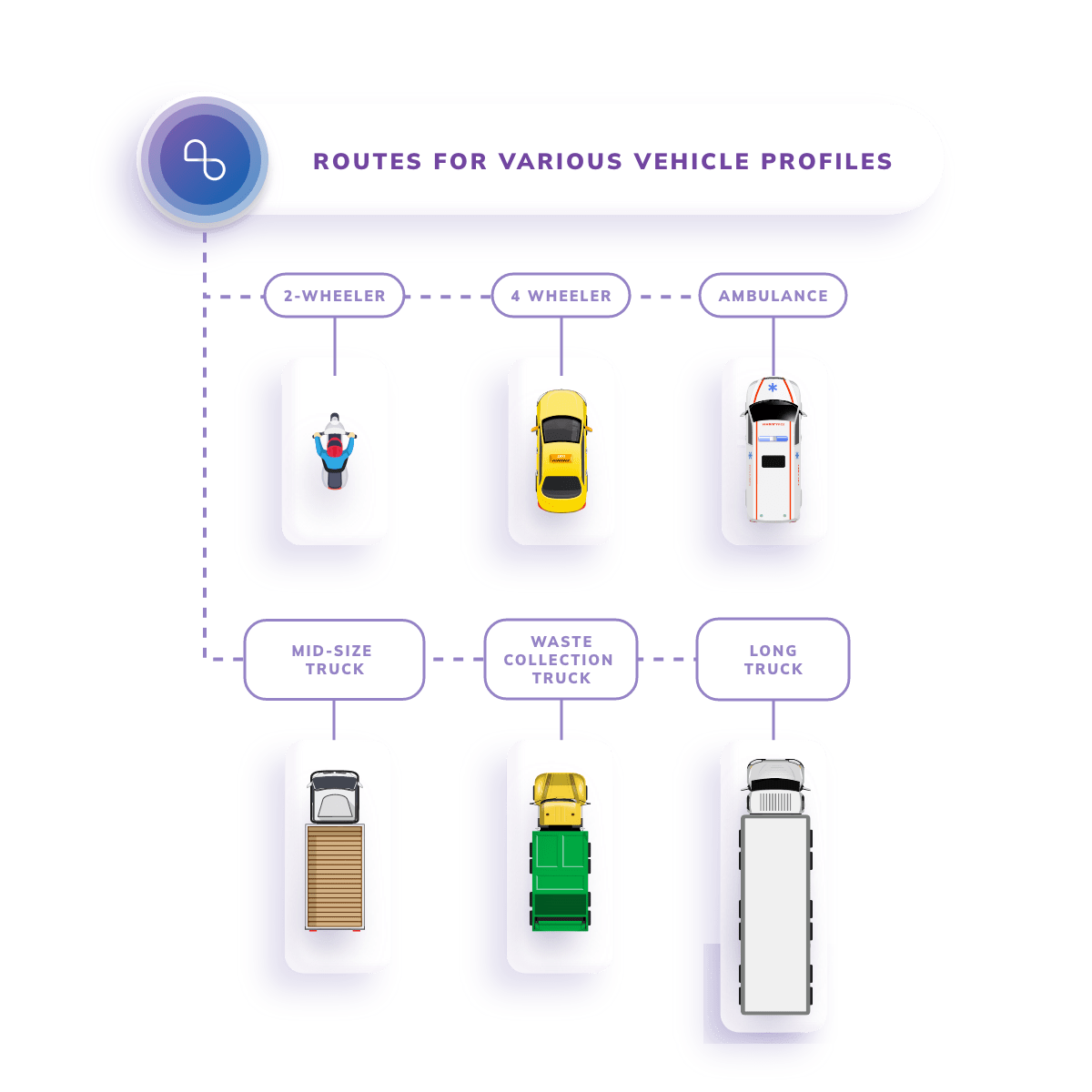
Support for Multiple Vehicle Types
Get precise ETA and distance predictions for all fleet types — cars, trucks, motorcycles and even mixed fleets.
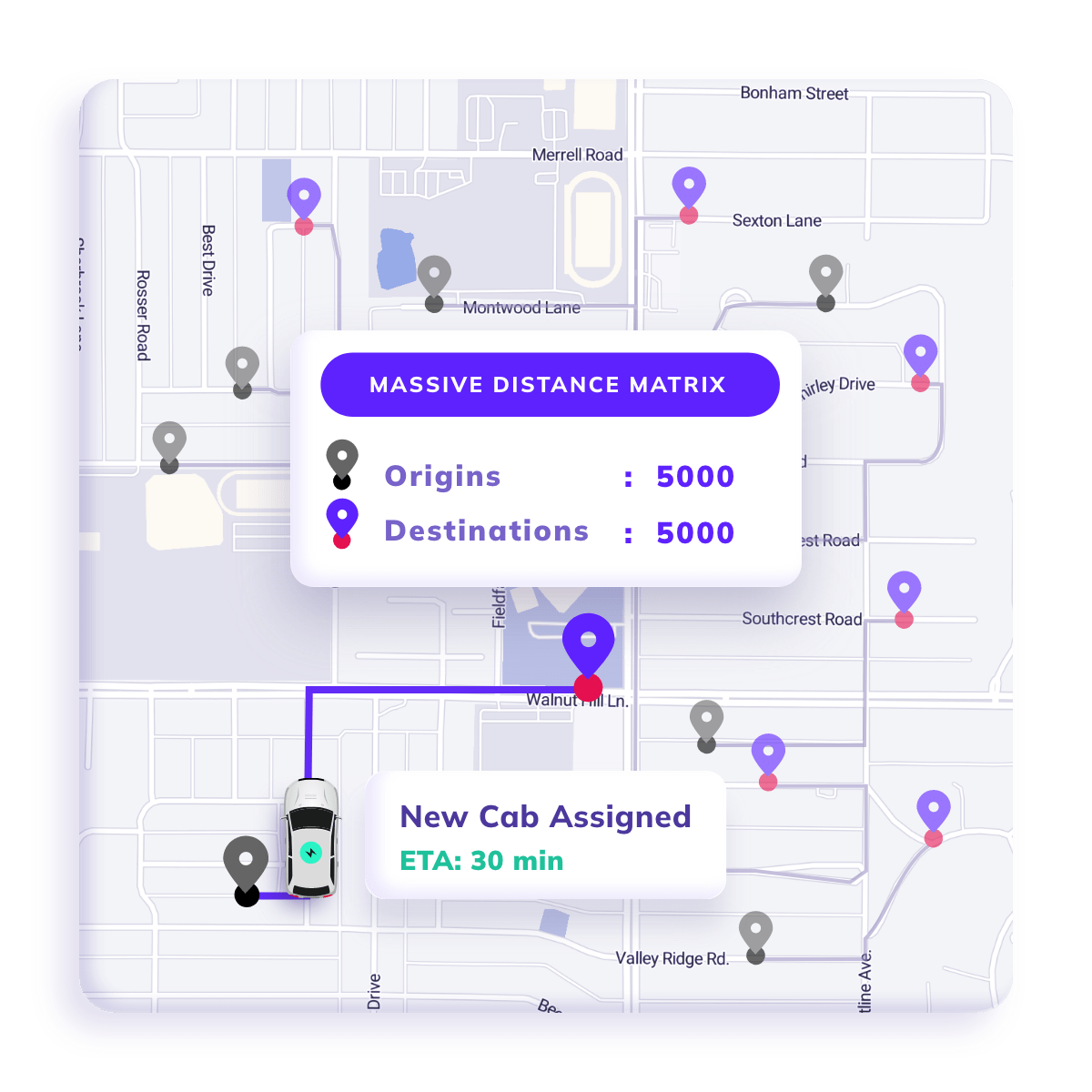
Large Matrix Size
Unlike the standard 25x25 matrix, NextBillion.ai’s API offers matrix sizes of up to 5000x5000 elements to handle large-scale operations with ease.
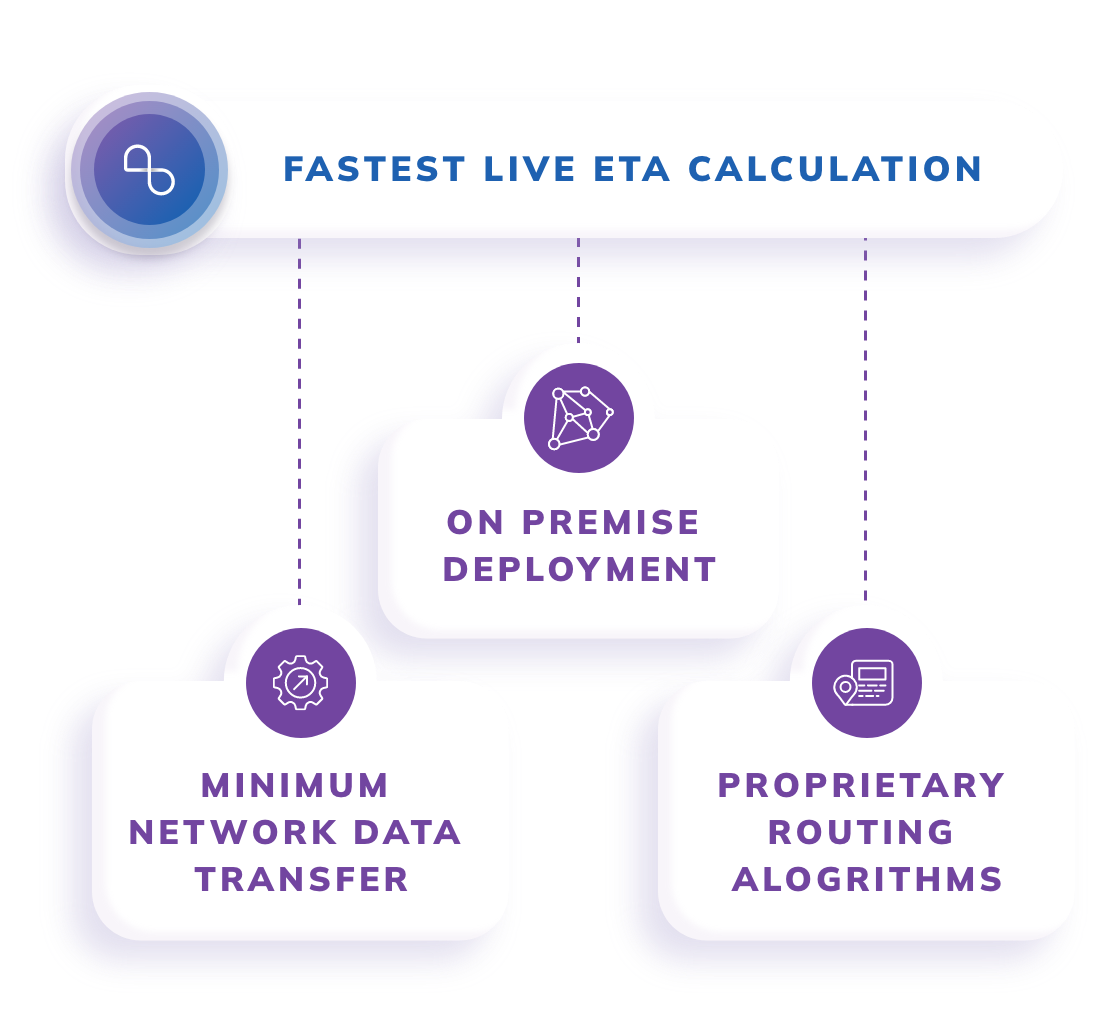
Low-Latency Operation
API performance is optimized to handle large matrices at very low latencies for time-sensitive use cases such as real-time dispatch.
Route Customization
Enforce your own time-dependent route customizations as per business needs — road closures, restricted zones, safety areas and more.
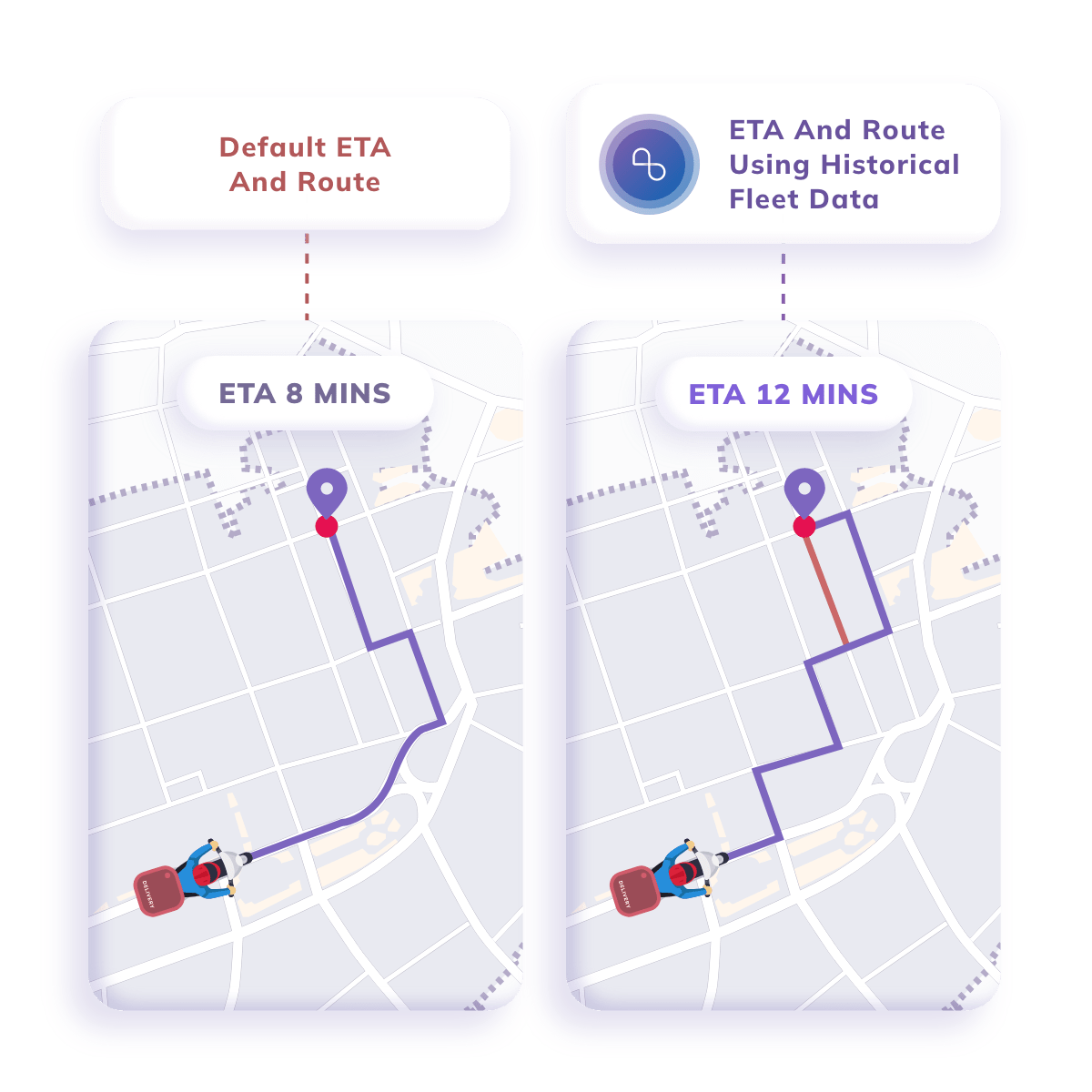
Ingestion of Proprietary Data
Feed our API with historical location data from your business operations for improved ETA accuracy and substantially lower costs.

Use Cases
Trusted by Enterprises and Start-Ups Worldwide










By substantially reducing the number of developer hours spent on scheduling, NextBillion.ai’s MVRP and large Distance Matrix API have helped us improve our operational efficiency and increase our cost savings significantly!

I admire NextBillion.ai's fast response and friendly manners whenever we need professional support in geospatial data processing. They have delivered a valuable service and support to our company that we appreciate.

NextBillion.ai solves the problem of providing a high-performance mapping platform at scale. We generate efficient delivery schedules in real time for hundreds of vehicles, so distance calculations need to be fast and reliable. NextBillion.ai’s Distance Matrix service meets and exceeds this demand.
How To Use
Distance Matrix API
Learn how our API plans better routes and schedules using our easy-to-follow documentation and tutorials.
Read API Docs Watch Demo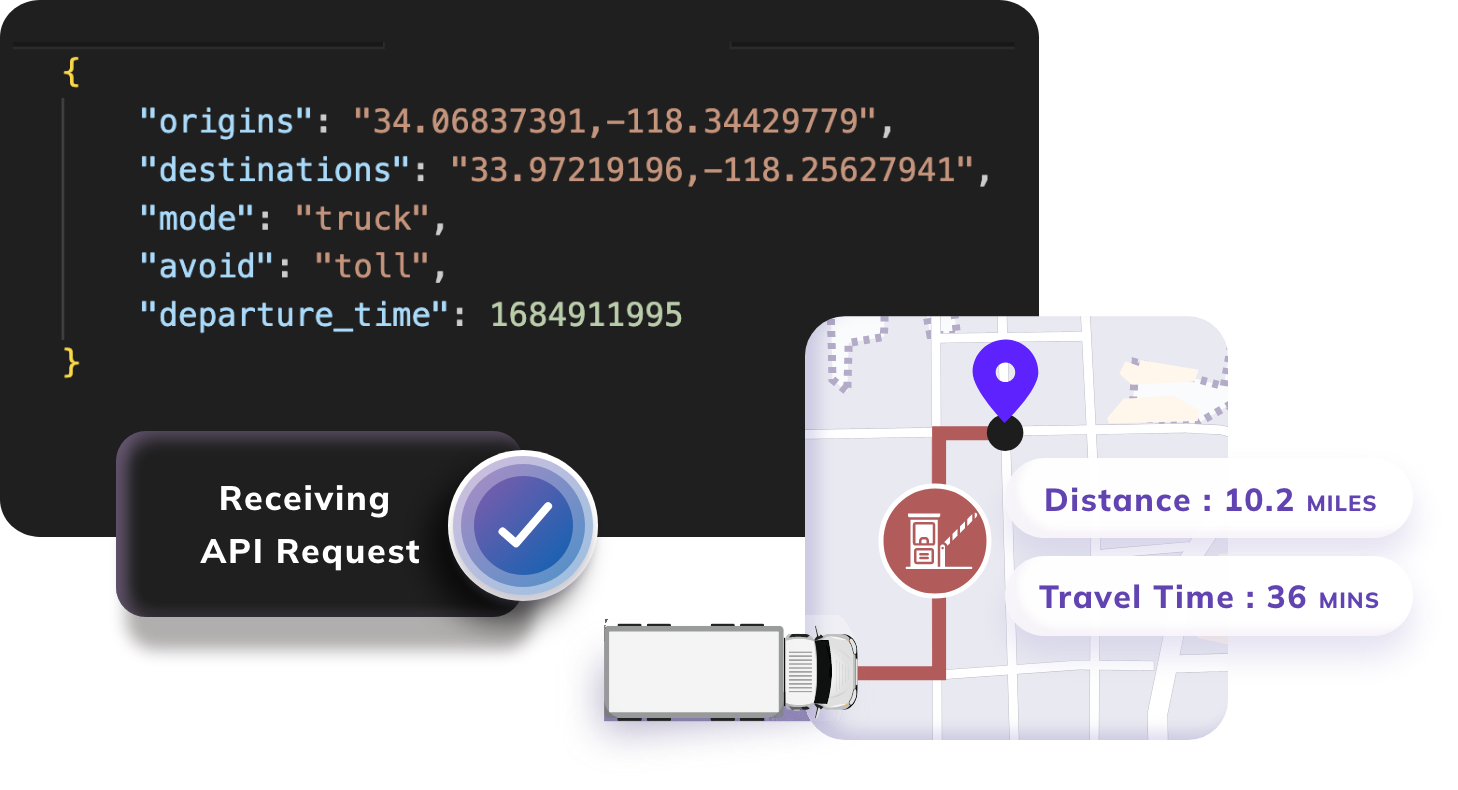
What Makes Us Unique

Ease of
Scaling
Our solutions are built for scale. Grow your business knowing that your location stack can keep up.

First-Party
Data Integration
Get the best possible results tailored to your operation by feeding historical data into our API.

Flexible
Pricing
We offer both asset-based pricing and usage-based pricing models. Pick what’s right for you.

Exceptional
Support
Our support team will be by your side at every step, from testing and integration to deployment and beyond.
Building Blocks for End-to-End Workflows
Explore a range of complementary APIs by NextBillion.ai that enable you to handle unique workflows.
Integrate Seamlessly With
Top Enterprise Clouds, ERPs and CRMs





FAQ
Distance Matrix is a two-dimensional array or square matrix representing distances between a set of locations. Each row and column in the matrix represents a location, and the cells store the distances or travel times between each pair of locations. This matrix gives a complete picture of the distances or travel times between all possible combinations of locations in a given area.
Distance matrices are widely used in logistics, transportation planning, and route optimization applications to determine the most efficient routes between multiple locations. They provide critical input data for algorithms and software systems that optimize vehicle routes, delivery services, and other transportation-related activities.
The following table represents a sample Distance Matrix.
| A | B | C | |
| A | 0 | 5 | 6 |
| B | 7 | 0 | 9 |
| C | 4 | 8 | 0 |
- The distance from A to A is 0, from A to B is 5, and from A to C is 6.
- The distance from B to A is the same as from A to B (5); from B to B, it is 0, and from B to C, it is 9.
- The distance from C to A is 4, from C to B is 8, and from C to C is 0.
Distance Matrix API service calculates distances and estimated time of arrival between the origin and destination pair for one-to-many and many-to-many scenarios.
Distance Matrix API is available in two versions – Fast and Flexible.
- Distance Matrix Fast API version returns distances and ETAs in real-time considering the usual traffic conditions at the time.
- Distance Matrix Flexible API version returns distances and ETAs based on additional parameters such as truck-specific routes, specific departure times, and a preference for the fastest or shortest route type.
Here are some common restrictions associated with NextBillion.ai’s Distance Matrix API:
- Usage Limits
- Distance Matrix Fast version: The API has a default limit of 1000x1000 origin-destination set which can be extended to 5000x5000 origin-destination set based on custom requests..
- Distance Matrix Flexible version: The API has a default limit of up to 50x50 Origin x Destination set, or 2500 elements and 8000 km total straight line distance between all the points in a request.
Contact[email protected] for information on higher limits.
- The HTTPS GET method of the Fast version can handle up to 100 locations, and the Flexible version can handle a total of 50 locations in a single request. In the case of large matrix sizes where the total number of locations is higher, the HTTPS POST method is recommended.
- Maximum dimensions allowed for truck size are 5000 cm for length, 5000 cm for width, and 1000 cm for height.
- The maximum weight allowed for a truck (including the trailer and shipped goods) is 100,000 kg.
- Rate Limiting: NextBillion.ai allows a maximum rate limit of 6000 queries per minute or 100 queries/second for continuous requests.
Note: Contact [email protected] to increase the quota based on the requirement.
The default units for the Distance Matrix API are as follows:
- Distance in meters.
- Duration in seconds.
- Time in UNIX format.
- Truck dimensions in centimeters.
Refer to Distance Matrix API Documentation for more details.
A distance matrix is a table that illustrates how far apart two points or locations are. It is a symmetric matrix in which each item in the `i`th row with the `j`th column reflects the distance between points i and j.
Here are the main factors to remember while reading a distance matrix:
- Symmetry: A distance matrix is symmetric, which means that the distance between points A and B is the same as between points B and A. As a result, the matrix is symmetrical along its primary diagonal.
- Values of the diagonals: The diagonal elements of the matrix contain the distances between a point and itself, with the row index (i) equal to the column index (j). These values are usually zero, reflecting the common notion that the distance from a point to itself is zero.
- Off-Diagonal Values: The off-diagonal elements represent the distances between different pairs of points. For example, the entry in the i-th row and j-th column is the distance from point i to point j.
Let's look at a simple example of a 3x3 distance matrix:
| A | B | C | |
| A | 0 | 5 | 6 |
| B | 7 | 0 | 9 |
| C | 4 | 8 | 0 |
In this matrix:
- The distance from A to A is 0, from A to B is 5, and from A to C is 6.
- The distance from B to A is the same as from A to B (5); from B to B, it is 0, and from B to C, it is 9.
- The distance from C to A is 4, from C to B is 8, and from C to C is 0.
Reading a distance matrix becomes more useful in network analysis, logistics, and other situations where knowing the relationships or distances between multiple sites is critical.
Many alternative methods of computing distance (distance metrics) have been developed. For example, city block distance, or Manhattan distance, estimates the distance between two points based on the sum of horizontal and vertical distances.
A distance matrix has to be specified in a form compatible with the study topic. For example, city block distance (or, better yet, the time it takes to go between each place) may be acceptable when grouping crime sites in a city. Where there is no theoretical reason for an alternative, the Euclidean should be favored because it is usually an adequate distance measure in the physical world.
Here's an example of a time distance matrix:
| A | B | C | |
| A | 0 | 5 | 6 |
| B | 7 | 0 | 9 |
| C | 4 | 8 | 0 |
- The entry in the first row and second column (15) represents the time it takes to travel from A to B.
- The entry in the second row and third column (20) represents the time it takes to travel from B to C.
- The diagonal entries are zeros, indicating negligible travel time from a point to itself.
A distance matrix algorithm is a method for calculating and expressing the pairwise distances between a collection of objects or points in a dataset as a matrix. The objects can range from data points in a multidimensional space to biological sequences, and the distances can be determined through a variety of metrics such as Euclidean distance, Manhattan distance, cosine similarity, and so on.
The distance matrix isa square matrix in which every component (i, j) illustrates the dissimilarity or distance between the ith and jth objects. The diagonal elements (i, i) can often be populated with zeros, representing the distance between an item and itself.
Depending on the nature of the data and the specific distance metric utilized, different algorithms and techniques are used to generate the distance matrix. Among the most common distance matrix algorithms are:
- The Euclidean distance: The straight-line distance between two places in Euclidean space is measured as the Euclidean distance.
- The Manhattan Distance: The Manhattan Distance, also known as the L1 distance or city block distance, is calculated by adding the absolute differences between two places' coordinates.
- Cosine Similarity: It is a measure that computes the cosine of the angle between two vectors. It is widely used in text mining and natural language processing to gauge the similarity between them.
- Hamming Distance: Used for binary data, it measures the number of positions at which the corresponding bits are different.
- Levenshtein Distance (Edit Distance): The number of single-character edits required for converting one string to another is frequently utilized in string matching.
- Minkowski Distance: The Minkowski distance is a generalization of both the Euclidean and Manhattan distances, with the parameter "p" defining the kind of distance (p=1 for Manhattan, p=2 for Euclidean).
Ready to
Get Started?
Seamlessly integrate NextBillion.ai's Distance Matrix API into your applications.
Request a Demo Read API Docs